This is an advanced guide on how to calculate Crossover Rate with detailed interpretation, analysis, and example. You will learn how to use its formula in capital budgeting analysis.
What is The Crossover Rate?
Crossover rate is the rate or level of return of two comparable projects that have the same net present value.
Since companies have limited resources, they must decide how to use these limited resources on various projects.
Calculating the crossover rate helps organizations choose which project to pursue by comparing their relative performance and evaluating the prospective profits against the risk factors.
An important factor in the computation of the crossover point is the net present value (NPV), which is calculated using a net present value formula.
The NPV in turn is determined by calculating the present value (PV) of the total costs and revenues of a project. The value is then discounted to adjust the future cash flows.
Some companies use net present value profile or graph to better aid management in its decision-making.
Crossover Rate Formula
First Project: Project X has an expected cash flow of CF1, CF2 and CF3 at the end of years 1, 2 and 3, respectively. It has an initial capital of A.
Using this data, the net present value equation for Project X is written as follows:
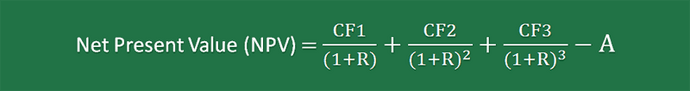
Second Project: Project Y has an expected cash flow of CFi and CFii at the end of years 1 and 2, respectively. It has an initial capital of B.
Using this data, the NPV equation for Project Y is written as follows:
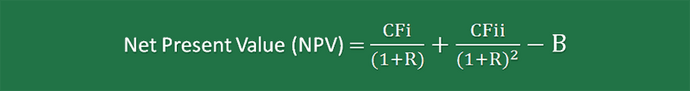
We can find the crossover rate of the two projects by equating the NPV equation for Project X with the NPV equation for Project Y and then calculating the rate.
The crossover point formula looks like this:
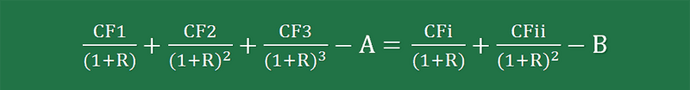
Once we have the data for the two projects, we can now solve the crossover rate or the cost of capital using a crossover rate formula.
Another way to compute the crossover rate is by using the internal rate of return or IRR, which measures the return on investment based on the initial capital and subsequent cash inflows.
The method is as follows:
- Calculate the cash flows for the first and second projects
- Calculate the difference between the (a) initial capital of both projects and (b) each periodic cash flows.
- Compute the IRR by equating the net present value equation of the resulting differential cash flows to zero.
- Compute the crossover rate
Example – How To Find Crossover Rate
Company ABC are looking to expand its core business by implementing two new projects.
The Project A with an expected capital outlay of $42 million and revenues of $32 million, $27 million and $19 million for the first, second and third year respectively.
The Project B with an expected capital investment of $60 million and revenues of $148 million by end of the third year.
What is the crossover rate for these two projects?
To solve the crossover rate, we have to subtract the cash inflows of the jet propulsion project from the metallurgy project to arrive at the following cash flows stream:
Initial cash investment = $60 million - $42 million = $18 million
Year-1 Cash flow = 0 – $32 million = -$32 million
Year-2 Cash flow = 0 - $27 million = -$27 million
Year-3 Cash flow = $148 million - $19 million = $129 million
Based on the given data, we can develop an IRR equation as follows:
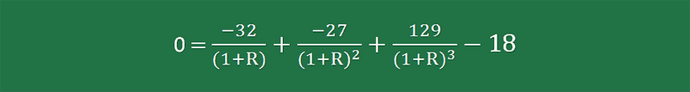
By setting X = 1 + R, we will have the revised equation, like so:
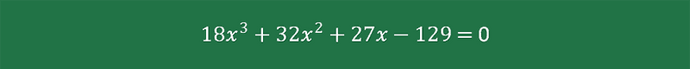
Use a math calculator to solve this equation, then we will have the value of X equal to 1.3014
X = 1.3014
Since we set X = 1 + R earlier, we need to subtract X by 1 to come up with the value of R:
Crossover Rate = X – 1 = 0.3014 or 30.14%
The crossover rate for the equation above is 30.14%.
This simply means that Stark Industries should go for the Project A as long as the cost of capital is less than 30.14%.
If it exceeds that rate, the Project B is preferable because it will provide a higher net present value.

